「コイン投げを行なって表と裏の出た回数を記録する実験を行っている途中で、裏の出た割合が高い時に、次からのコイン投げでは表が出やすいのか」ということが、毎週、金曜日に開催している犬4匹本の輪読会で、議論になりました。
この問の考え方はギャンブルをやる時などに、とても役立つ考え方なので整理しておきます。
以下、「問題」に状況を具体的に書きました。「問題」に解答した上でその後の文章をお読みいただければと思います。(この記事は、解答がすぐにわかり、大数の法則を理解している方は、読む必要がない内容だと思います。)
「問題」
問1
表と裏のでる確率が半々である、ゆがみのないコインがあります。
このコインを200回投げて、表が出た回数と裏が出た回数を記録します。
100回コイン投げをした時点で、表が20回、裏が80回という結果になりました。
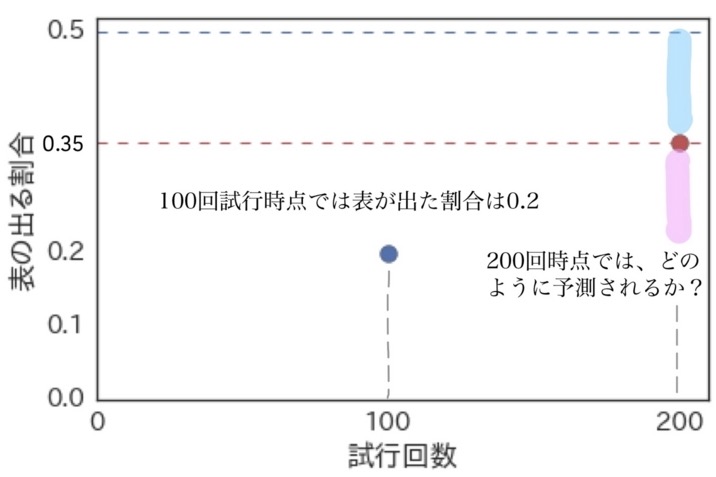
残り100回のコイン投げでは、表がでる回数は何回と見込まれるでしょうか(期待値はいくつでしょうか)、
以下の3択から選んでください。
- 50回より多い (合計70回より多く、下図の水色の部分のいずれか)
- 50回 (合計70回で表の割合0.35、下図の赤丸)
- 50回より少ない (合計70回より少なく、下図のピンクの部分のいずれか)
問2
コイン投げの結果は試行を多くすれば期待値に「収束」するということを聞いたことがあると思います。収束するのであれば問1の解答は「1. 50回より多い」になるのではないでしょうか?
解答
問1解答
- 50回(合計70回)
問2解答例
「収束」という意味は試行を増やせば、表がでる割合がいくらでも0.5に近づくということである。
100回試行した時点で裏が多かったから、残りの100回が表が出やすくなって表がでる割合が0.5に近づくということではない。
補足
コイン投げで表の出る確率は、前のコイン投げの結果に影響をうけないので、「2. 50回」が解答となります。
また、「期待値に収束」するというのは、試行回数を増やせばいくらでも期待値に近づけられることを言います。
100回コインを投げた時点で、20回表がでたという状況から、試行回数を増やすとどうなるかプログラム(python)でやってみた図が以下です。追加で100回、1000回、10,000回と試行を増やすにつれ、割合は少しずつ0.5に近づいていき、追加で10,000回投げた時点では、ほとんど0.5に一致しているのがわかると思います。
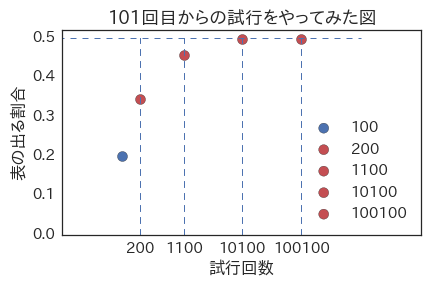
大数の法則
上記の理論は数学では「大数(たいすう)の法則」という定理で証明がされています。
数式や証明は省略しますが、確認したい方は大数の法則と中心極限定理の意味と関係 | 高校数学の美しい物語のブログがとても分かりやすいと思います。
私が以前に作ったスライドでも証明を書いたことがあるので、リンクを貼っておきます。
ギャンブルの考え方
この大数の法則の理論は、ギャンブル等の勝負事の考え方でも、大変重要なので少しだけ考え方と私が考えていることを書いておきます。
考え方
ギャンブルで大切なのは、1回1回の勝負のリターンの期待値が100%よりも高いのか、低いのかを、とにかく考えることです。
そして、期待値に応じて以下の戦略をとることです。
- 期待値が100%よりも高いのであれば、ひたすら勝負を続ける。(仮に途中まで負けていても期待値が100%を越えているのであれば、ひたすら続ける)
- 期待値が100%よりも低いのであれば、勝負しない。
結論として、勝負事で難しいのは、リターンの期待値が100%を超える勝負を探すということで、それがみつかればひたすら続けるだけで良いということです。
終わりに
書く前は、もう少しわかりやすい説明をできると思って書き始めたのてわすが、中々わかりやすい説明はできないものです。
もっとわかりやすい説明とか疑問点があれば、是非コメントに記載ください。
pythonのコード
途中の図を作ったpythonのコードはgithubとkaggleにあげておきました。
これをRで書いてくれたり、改良してくれたりするととても喜びます。
輪読会
今回の話はベイズ統計モデリング輪読会#2 - connpassでの第4章に関連した内容でした。
なお、次回の輪読会は以下です。